What is Goedel-Prover ?
Goedel-Prover is an open source AI model that focuses on the form proof generation of automated mathematical problems. The core objectives of this model are:
✅ Convert natural language math problems to formal language (such as Lean 4)
✅ Automatically generate complete mathematical proofs to solve the problem of scarcity of formal mathematical statements and proofs
✅ Improve the automatic proof ability of mathematical theorems and promote the development of AI in the field of mathematical reasoning
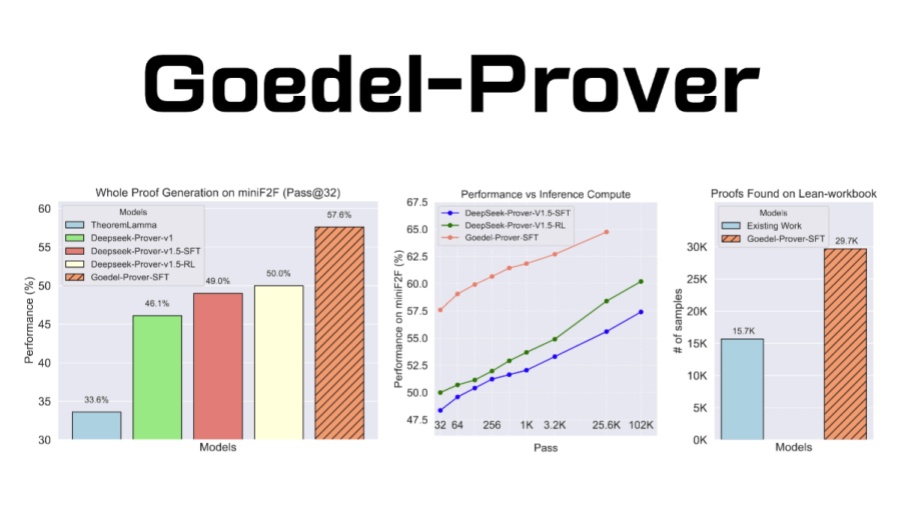
Goedel-Prover has achieved breakthrough results in several benchmarks, such as:
1.miniF2F benchmark test: success rate is 57.6%, surpassing all previous open source models
2.PutnamBench: Successfully solved 7 difficult math problems
3.Lean Workbook: Automatically generate nearly 30,000 formal proofs
Core functions
✅ 1. Formal translation
Automatically analyze natural language mathematical problems and accurately convert them to Lean 4 formal languages
Ensure the logical integrity and mathematical rigor of translation
✅ 2. Automatic theorem proof
Generate a complete mathematical proof process based on AI automatic reasoning
Suitable for advanced mathematics, computer science and other fields
✅ 3. Expert Iteration Training
Using expert iterative methods to perform multiple rounds of optimization to continuously improve mathematical proof ability
Verify the correctness of the proof using the Lean compiler to ensure that the generated proof is rigorous
✅ 4. Large-scale dataset training
Combining Numina, Lean Workbook, Mathlib4 and other data sets to enhance generalization capabilities
Continuously expand the mathematical problem bank during the training process to adapt to different mathematical fields
Technical Principles
✅ 1. Formal translation
Formalizer A & B: Two different styles of mathematical translation to improve diversity
Compile Correctness (CC) Test: Ensure formal statements comply with Lean syntax
Fidelity and Completeness (FC) Test: Ensure that translations accurately express original mathematical problems
✅ 2. Expert iterative training
Use DeepSeek-Prover-V1.5-RL to generate initial proof
Verify correctness through Lean compiler and filter high-quality proofs
Training data is continuously updated, model is continuously optimized, and automatic proof ability is improved
✅ 3. Dataset extension
Combining external datasets such as Numina and Mathlib4, enriching the mathematical theorem library
Gradually increase Lean Workbook data during training to improve adaptability in different math fields
Application scenarios
Mathematical research: Help mathematicians to verify complex theorems and accelerate research progress Mathematical teaching: Provide teachers with detailed mathematical proofs to assist students in understanding mathematical logic software verification: used to verify the correctness of software algorithms, improve safety and reliability
AI algorithm verification: Ensure the mathematical theoretical foundation of AI-related algorithms is reasonable and rigorous interdisciplinary research: Supporting the application of mathematical reasoning in physics, engineering and other disciplines
Goedel-Prover Project Address
GitHub repository: Goedel-Prover
HuggingFace Model Library: Model Download
arXiv Paper: Technical Report